GPT-4数学准确率达到84.3%!港中文、清华等七所顶尖高校提出创新的CSV方法
 发布于2023-10-01 阅读(0)
发布于2023-10-01 阅读(0)
扫一扫,手机访问
虽然大型语言模型(LLMs)在常识理解、代码生成等任务中都取得了非常大的进展,不过在数学推理任务上仍然存在很大改进空间,经常会生成无意义、不准确的内容,或是无法处理过于复杂的计算。
最近推出的一些语言模型,如GPT-4和PaLM-2,在数学推理方面取得了重大进步。尤其是OpenAI最新版本的模型GPT-4 Code Interpreter,在较为复杂的数学推理数据集上展现出了出色的性能
为了探索「代码生成任务」对「语言模型推理能力」的影响,来自香港中文大学、南京大学、中国科学技术大学、清华大学、香港城市大学、长沙理工大学和塔夫茨大学的研究人员联合发布了一篇论文,通过在代码使用频率(Code Usage Frequency)上引入不同的约束限制进行实验验证。

论文链接:https://arxiv.org/abs/2308.07921
实验结果显示,GPT-4 Code Interpreter模型的成功在很大程度上要归功于「在生成和执行代码、评估代码执行的输出以及在收到不合理的输出」时纠正其解决方案方面的强大能力。
基于上述结论,研究人员提出了一种新颖且高效的提示方法,显式的基于代码的自我验证(CSV, code-based self-verification),以进一步提高GPT-4代码解释器的数学推理潜力。
该方法在GPT-4 Code Interpreter上采用zero-shot提示,以促使模型使用代码来对答案进行自我验证。
在验证状态为「假」的情况下,模型将自动修改其解决方案,类似于人类在数学考试中纠错的过程。
此外,研究人员还发现验证结果的状态可以指示解决方案的置信度,并进一步提高多数表决的有效性。
通过结合GPT-4 Code Interpreter和CSV方法,在MATH数据集上的零样本准确率实现了从54.9%到84.3%的显著提升
LLM的推理能力从何而来?
为了研究GPT4-Code对解决数学问题的能力受代码使用的影响,研究人员采用了一种直接的方法,即通过设计精心的提示来限制GPT4-Code与代码的交互
具体包括两种代码限制提示以及一种基础提示用来对比:

重写内容:提示1:禁止使用代码
GPT4-Code不允许在其解决方案中添加代码,也就是说模型只能完全依赖自然语言(NL)推理链,类似于思维链(CoT)框架中的解决方案,由此产生的推理步骤序列叫做CNL,如上图中(a)所示。
重写内容:请注意:代码只能使用一次
GPT4-Code只能用单个代码块内的代码来生成解决方案,类似于之前的PAL方法,论文中将此序列称为CSL,即使用符号语言(SL),如Python进行推理,上图中(b)为样例。
重写内容:基本提示:对于代码的使用没有任何限制
推理序列可表示为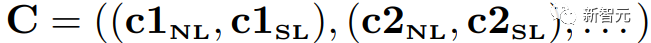 ,其中每个步骤都由自然语言和 Python 代码组成,示例如上图中(c)所示。
,其中每个步骤都由自然语言和 Python 代码组成,示例如上图中(c)所示。
在这项研究中,除了以上所述的内容,研究人员还考虑了代码使用频率对不同提示下代码执行次数的影响。他们发现,GPT4-Code的高性能与高代码使用频率之间存在正相关关系
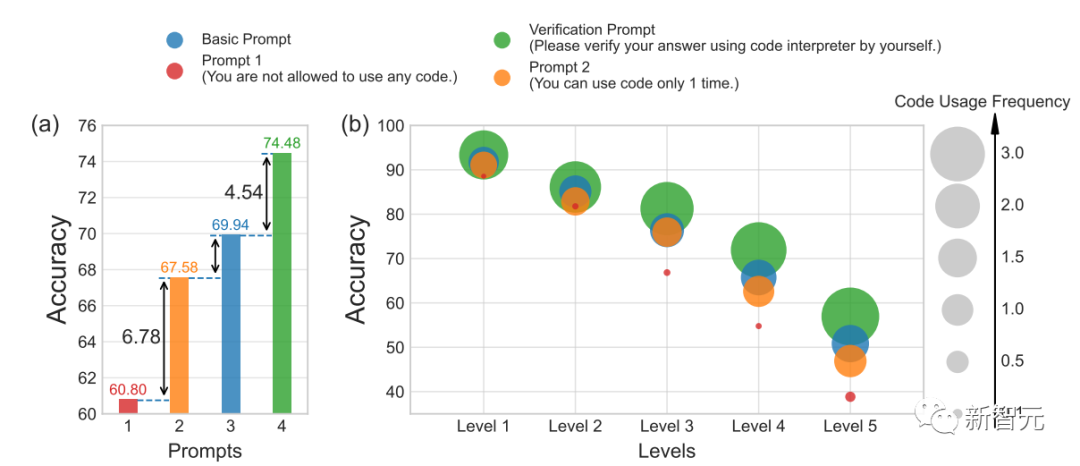
具体来说,提示2的代码量是提示1的两倍,并且提示2的准确率比提示1提高了6.9%。这表明使用Python代码链CSL比自然语言链CNL更能提高计算能力。这个观察结果与之前基于Python的提示方法的结果一致
然而,只能使用一次的代码存在一些缺陷。当代码输出出现错误或产生意外结果时,模型无法自我调试
在对比提示2和基本提示时,可以发现,基本提示始终能生成包含多个代码使用实例的解决方案,即代码使用频率更高,并且基本提示的准确性也明显提高。
具体可以归因于代码的两个优势有以下几点:
1. 生成一些简短的代码块,可以分割自然语言推理步骤,从而带来更高的准确率;
2. 模型有能力评估代码执行结果,并在结果中发现错误或不合逻辑的解决步骤,并进行修正。
基于代码的自验证CSV
通过对代码使用频率分析观察结果的启发,研究人员决定利用GPT4-Code的代码生成、代码评估、代码执行以及自动调整解决方案等能力,以增强方案验证并提高推理性能
CSV的主要流程是通过对GPT-Code输入提示进行代码生成来验证答案的正确性
对于验证方案C的结果V,可以分为三类:真、假、不确定
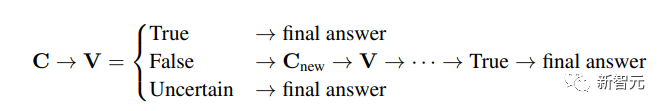
将CSV与模型结合后,我们可以使用代码来验证答案。如果验证结果显示为“错误”,我们可以审查并调整解决方案,以获得正确答案

在对初始解决方案进行完善和修正之后,准确率可以得到明显的提升
需要注意的是,验证和修正阶段都是基于代码的,因此必然会导致代码的使用频率增加
在 GPT4-Code 出现之前,先前的框架大多依赖于外部LLM使用自然语言进行验证和精心设计的少样本提示。
相比之下,CSV方法仅依赖于GPT4-Code的直接提示,以零样本的方式简化了流程,利用其先进的代码执行机制来自主验证和独立修正解决方案。
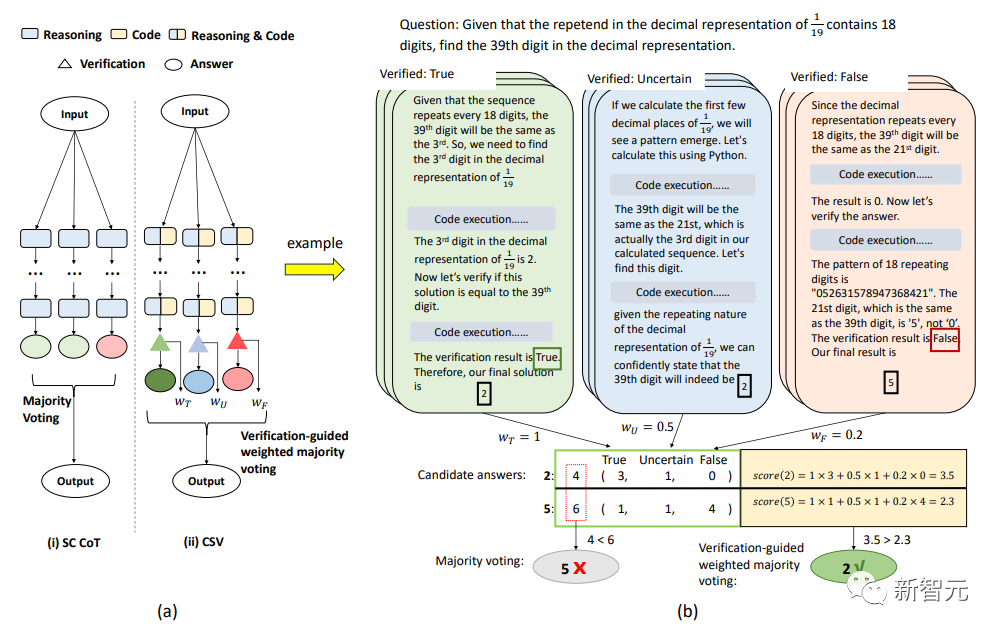
研究人员还将验证阶段集成到了加权多数表决中,为验证过程的各个状态分配了不同的权重
为了防止答案被确认为「假」后不再进行其他验证,研究人员将三种状态分配了不同的权重:wT, wF和wU,可以增加系统的可靠性。
为了简单起见,集成算法从k个解决方案中提取一对最终答案及其相应的验证结果,表示为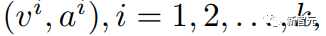 其中v和a分别代表第i个最终答案和最终验证结果。
其中v和a分别代表第i个最终答案和最终验证结果。
所以,候选答案 a 的投票得分可以用以下方式表示:
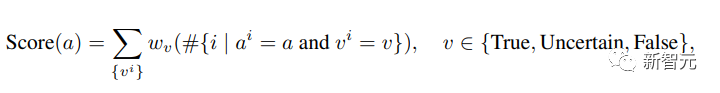
最终,从所有候选答案中选择得分最高的答案:

实验结果
MATH数据集
GPT4-Code在MATH基准上的准确率达到了69.69%,明显超过了之前的方法(53.90%),这表明GPT4-Code在解决数学问题方面展现出了强大的能力
在GPT4-Code的基础上,文中提出的CSV方法进一步提高了准确性,将准确率提高到了73.54%;
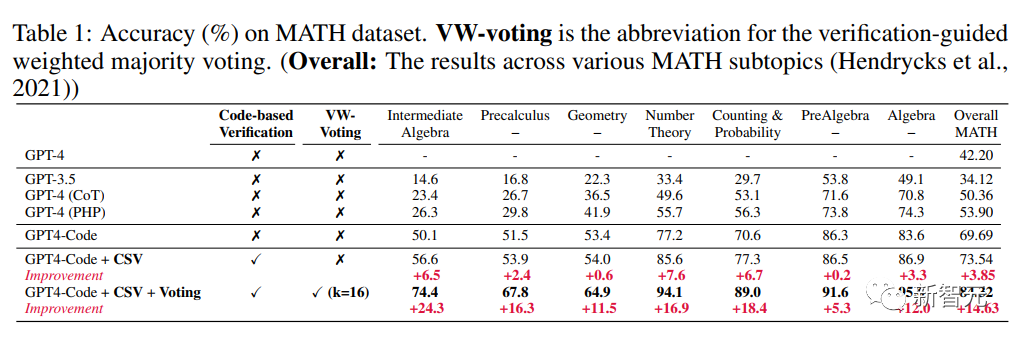
在加入基于代码的显式自我验证和验证引导的加权多数投票(采样路径数为 16)后,结果进一步提高到了84.32%
需要注意的是,尽管增加基于代码的自我验证可以提高题目的得分,但具体程度会因题目的难度和形式而有所不同
其他数据集
研究人员还在其他推理数据集上应用了CSV方法,包括GSM8K、MMLU-Math和MMLU-STEM
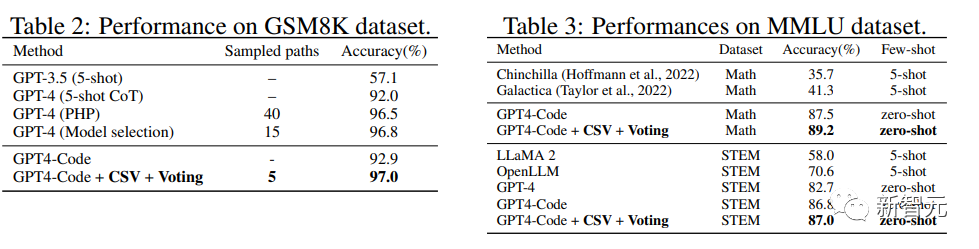
从结果上来看,CSV+GPT4-Code在各个数据集上都取得了最优的结果。
与带有模型选择功能的GPT-4和 PHP相比,验证引导的多数表决是减少采样路径数量的有效框架。
在MMLU-Math和MMLU-STEM数据集上进行的CSV方法与现有模型的性能对比显示,开源模型明显优于闭源模型
为了弥补这一差距,研究人员表示目前已经开始着手准备制作数据集,并将在不久的将来公开发布。
其他开源LLM模型,例如LLaMA 2,可以使用这个数据集进行微调,从而进一步提高数学推理能力
产品推荐
-

售后无忧
立即购买>- DAEMON Tools Lite 10【序列号终身授权 + 中文版 + Win】
-
¥150.00
office旗舰店
-

售后无忧
立即购买>- DAEMON Tools Ultra 5【序列号终身授权 + 中文版 + Win】
-
¥198.00
office旗舰店
-

售后无忧
立即购买>- DAEMON Tools Pro 8【序列号终身授权 + 中文版 + Win】
-
¥189.00
office旗舰店
-

售后无忧
立即购买>- CorelDRAW X8 简体中文【标准版 + Win】
-
¥1788.00
office旗舰店
-
 正版软件
正版软件
- 币圈冷钱包是什么
- 冷钱包是一种与互联网隔离的数字货币存储设备,可防止网络攻击和黑客入侵,为数字资产提供安全保障。它通常以硬件设备或纸质介质的形式存在,可安全存储数字货币,避免黑客远程访问,并提供多种类型,包括硬件冷钱包、纸质冷钱包和离线多重签名钱包。
- 7分钟前 0
-
 正版软件
正版软件
- 黄立成发Meme币!Bobaoppa十小时狂吸3500万美元SOL
- 本站(120bTC.coM):曾经言论创币会爆冲的麻吉大哥发币了!3月28日,麻吉大哥宣布,在Solana推出一个名为Bobaoppa的Meme币预售,并同时开始募资。该项目的总供应量为1亿枚,起始募资目标设定每位用户最低1SOL、最高上限是1,000SOL。另外据了解,Bobaoppa是麻吉大哥饲养的狗儿子。募资金额达19.6万颗SOL投资者需要密切关注Meme币的波动性,及时报告以高频度伴随着高风险。投资者在参与这类项目时应充分考虑市场波动性,谨慎投资。
- 27分钟前 元宇宙 Web3.0 Arbitrum 比特币爆仓 中币/ZB网 0
-
 正版软件
正版软件
- ETHFI币是谁创建的?ETHFI币值得投资吗
- Ether.Fi允许参与者在代理质押时保留对其密钥的控制。存款到Ether.Fi会自动与Eigenlayer再质押。Ether.Fi(ETHFI币)是一个以太坊上全新的基础设施型质押协议。Eigenlayer利用质押的ETH支持外部系统(如rollups、预言机),建立一个经济安全层,这在过程中增加了ETH质押者的收益。ETHFI币是谁创建的?ETHF币是目前火热的数字货币之一,这款虚拟货币的创始人是MatthijsVanSchelven。ETHFI币价格最新行情$4.04≈¥29.1
- 42分钟前 虚拟货币 区块链 比特币 ETHFI币 0
-
 正版软件
正版软件
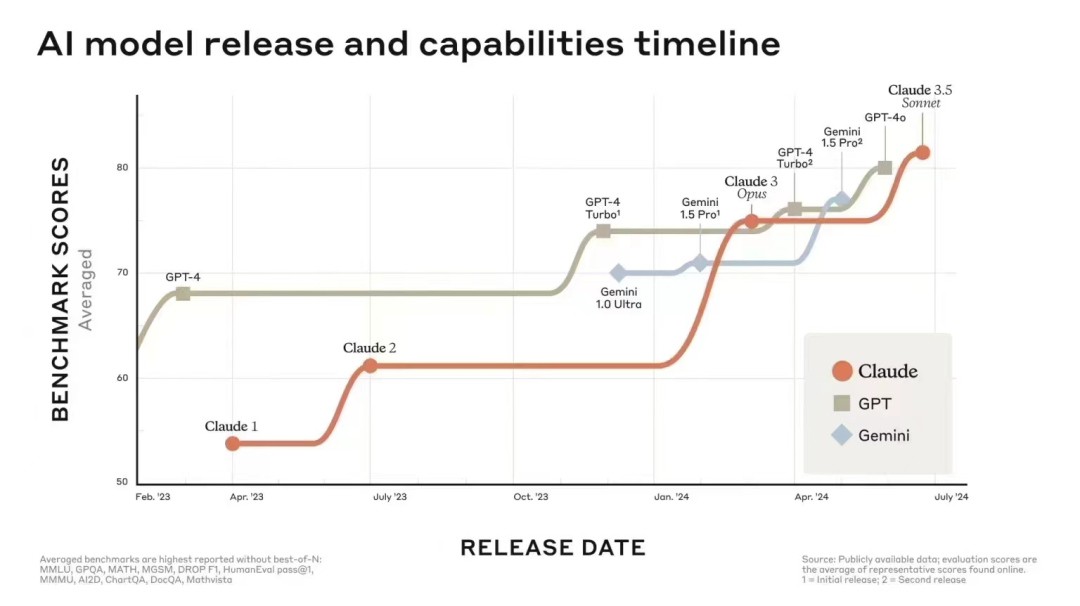
- 谷歌「诚意之作」,开源9B、27B版Gemma2,主打高效、经济!
- 性能翻倍的Gemma2,让同量级的Llama3怎么玩?AI赛道上,科技巨头们激烈角逐。前脚有GPT-4o问世,后脚就出现了Claude3.5Sonnet。如此激烈的争斗中,谷歌虽然发力较晚,但在短时间内就能有显著的能力跟进,可见其技术发展与创新的潜力。除了Gemini模型外,Gemma这一系列轻量级的SOTA开放模型似乎与我们距离更近。它基于Gemini模型相同的研究和技术构建,旨在让每个人都拥有构建AI的工具。谷歌持续扩展Gemma家族,包括CodeGemma、RecurrentGemma和PaliGe
- 57分钟前 谷歌 产业 Gemma 2 0
-
 正版软件
正版软件
- Web3.0时代是一个什么时代
- Web3.0时代以去中心化、独立自主和协作性为主要特征,代表着互联网从以公司为中心的向以用户为中心的转变。它的核心原则是:去中心化:数据和应用程序分散在整个网络中,消除单点故障风险。独立自主:用户拥有对其数据的控制权,积极参与塑造互联网未来。协作性:分布式账本技术促进协作和社区建设,创造创新机会和全球协作。
- 1小时前 17:50 0
最新发布
-
 1
1
- 阿里追捧的中台,“热度”退了?
- 1984天前
-
 2
2
- Overture设置踏板标记的方法
- 1821天前
-
 3
3
- 思杰马克丁取得CleanMyMac中国区独家发行授权
- 1811天前
-
 4
4
- IBM:20万台Mac让公司职工在工作中更快乐 更多产
- 2009天前
-
 5
5
- 报道称微软一直在悄然游说反对“维修权”立法!
- 1975天前
-
 6
6
- 美国怀疑华为窃取商业机密 华为:身正不怕影子斜
- 1971天前
-
 7
7
- 三星被曝正与联发科接洽 A系列手机有望搭载其5G芯片
- 1986天前
-
 8
8
- 环球墨非完成千万级融资 联合企业集团投资
- 2007天前
-
 9
9
相关推荐
热门关注
-

- Xshell 6 简体中文
- ¥899.00-¥1149.00
-

- DaVinci Resolve Studio 16 简体中文
- ¥2550.00-¥2550.00
-

- Camtasia 2019 简体中文
- ¥689.00-¥689.00
-

- Luminar 3 简体中文
- ¥288.00-¥288.00
-

- Apowersoft 录屏王 简体中文
- ¥129.00-¥339.00