SPSS使用方法:如何对时间序列数据进行因子分析
 发布于2024-12-14 阅读(0)
发布于2024-12-14 阅读(0)
扫一扫,手机访问
请教:时间序列如何用SPSS进行因子分析
因子分析
1输入数据。
为了帮助尚未过关的玩家,让我们一起来了解一下具体的解谜方法吧。首先,点击游戏界面上的“2点Analyze”下拉菜单,然后选择“Data Reduction”下的“Factor”选项。
为了开始解谜,我们需要打开Factor Analysis,并将数据变量逐个选择进入Variables对话框中,以便进一步分析。
单击主对话框中的"Descriptive"按钮,打开"Factor Analysis: Descriptives"子对话框。在"Statistics"栏中选择"Univariate Descriptives"项,以输出各个变量的均值和标准差。在"Correlation Matrix"栏内选择"Coefficients"项,以计算相关系数矩阵。然后单击"Continue"按钮,返回"Factor Analysis"主对话框。
为了帮助还没有过关的玩家们,让我们一起来了解一下具体的解谜方法吧。首先,点击主对话框中的Extraction按钮,打开Factor Analysis: Extraction子对话框。在Method列表中选择默认的因子抽取方法——Principal Components,在Analyze栏中选择默认的Correlation Matrix项,以便从相关系数矩阵出发解析主成分。在Exact栏中选择Number of Factors;6,这样可以显示所有主成分的得分和所能解释的方差。最后,点击Continue按钮返回Factor Analysis主对话框。
6单击主对话框中的OK 按钮,输出结果。
统计专业研究生工作室原创,请勿复杂粘贴
问spss的因子分析
Rotated Component Matrix是经过旋转后的因子负荷矩阵,它能帮助我们更好地理解数据之间的关系。
当你设置了因子转轴后,便会产生这结果。
转轴的目的是为了获得明确的负载形式,以便研究人员进行因素解释和命名。这样有助于帮助研究者更好地理解和解释相关因素。
在SPSS的Factor Analysis对话框中,你会注意到一个Rotation按钮。点击该按钮后,会弹出一个Rotation对话框。在这个对话框中,你可以进行因子旋转操作。这一步是非常重要的,因为旋转可以使得因子结构更加清晰和解释性更强。通过选择合适的旋转方法和参数,你可以调整因子的位置和相互关系,从而获得更好的解释和解谜结果。
其中有5种因子旋转方法可选择:
最大变异法(Varimax)是一种常用的因子分析方法,它的目标是使得因子内的负荷量变异数最大化。具体而言,这种方法会使得每个因子上具有最高载荷的变量数最少。通过使用Varimax方法,我们可以更好地理解和解释因子分析结果。
四次方最大值法(Quartimax)是一种解谜方法,旨在通过使负荷量的变异数在变项内最大化来确定每个变量中需要解释的因子数最少。该方法通常用于解决因子分析问题。在使用Quartimax方法时,我们可以通过计算每个变量的四次方最大值来确定最佳解释因子数。通过最大化负荷量变异数,我们可以有效地提取出主要的因子,从而更好地理解数据的结构和关系。
3. 相等最大值法(Equamax):结合前两种方法,最大化负荷量变异性在因素内和变项内的同时。这种方法可以平衡因素和变项之间的关系,以实现最大的解谜效果。
4. 直接斜交转轴法(Direct Oblimin):通过最小化因素负荷量的差积(cross-products),来进行因子旋转的一种方法。这种方法可以帮助我们更好地理解因子之间的关系,并使得因子结构更为清晰。它是一种常用的因子旋转技术之一。
5. Promax转轴法是一种解决因子间相关性的方法。首先使用直交转轴(varimax)方法得到初步的因子载荷矩阵。然后将这个结果用相关的斜交转轴再次进行转轴。通过将因子载荷量取2、4、6次方,可以得到接近0但不等于0的值,从而找出因子之间的相关性。这种方法在保持因素简化的特性的同时,能够解决因子间的相关性问题。
上述前三种方法被归类为"直交(正交)转轴法"(Orthogonal Rotations),这种方法中各个因子之间没有相关性,因子轴之间的夹角都是90度。而后两种方法则属于"斜交转轴"(oblique rotations),表示因子之间存在某种程度的相关性,因子轴之间的夹角不是90度。
直交转轴法的优点是因子之间提供的讯息不会重叠,受访者在某一个因子的分數与在其他因子的分數,彼此独立互不相关;缺点是研究迫使因素之间不相关,但这种情况在实际的情境中往往并不常存在。至於使用何种转轴方式,须视乎研究题材、研究目的及相关理论,由研究者自行设定。
在解释因子的结果时,除了要观察因子负荷矩阵中哪些变量与因子具有高负荷,哪些变量与因子具有低负荷外,还需要注意之前所使用的转轴方法所代表的含义。
下一篇:禁用Win10的实时防护
产品推荐
-

售后无忧
立即购买>- DAEMON Tools Lite 10【序列号终身授权 + 中文版 + Win】
-
¥150.00
office旗舰店
-

售后无忧
立即购买>- DAEMON Tools Ultra 5【序列号终身授权 + 中文版 + Win】
-
¥198.00
office旗舰店
-

售后无忧
立即购买>- DAEMON Tools Pro 8【序列号终身授权 + 中文版 + Win】
-
¥189.00
office旗舰店
-

售后无忧
立即购买>- CorelDRAW X8 简体中文【标准版 + Win】
-
¥1788.00
office旗舰店
-
 正版软件
正版软件
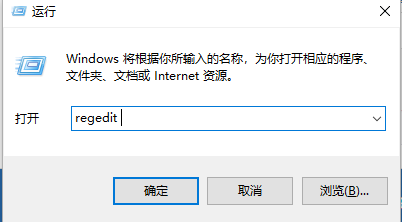
- win11开始菜单变小了怎么办?win11开始菜单变小了问题解析
- 我们在使用win11系统的时候有时候需要使用到开始菜单,但是也有不少的用户们表示开始菜单变小了怎么办?用户们可以直接的进入到注册表编辑器下的Advanced文件夹来进行操作就可以了。下面就让本站来为用户们来仔细的介绍一下win11开始菜单变小了问题解析吧。win11开始菜单变小了问题解析1、首先右击下面的开始菜单,然后选择“运行”(如图所示)。2、在运行中输入:regedit,点击确定(如图所示)。3、进入注册表后依次展开到:HKEY_CURRENT_USER\Software\M
- 4分钟前 win11 0
-
 正版软件
正版软件
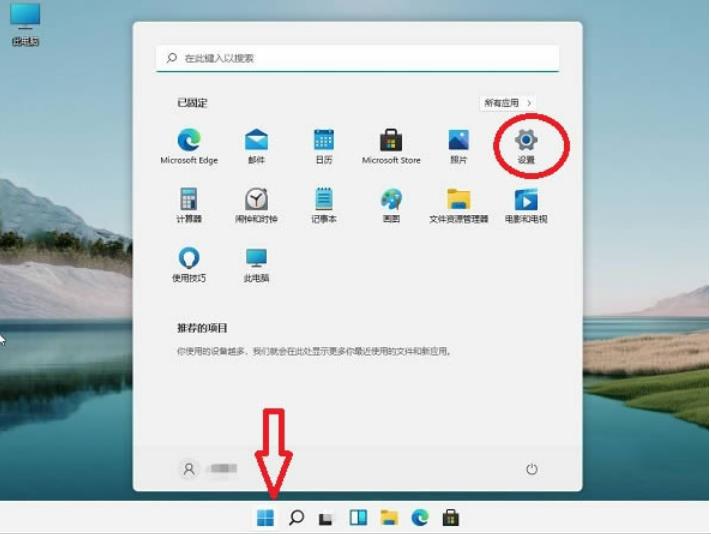
- win10怎么删除右键图形属性?win10删除右键图形属性方法
- 最近许多win10用户在打开右键菜单的时候,发现出现了图形属性的按钮,这个一般是我们的集成显卡,很多人都不会去使用,在右键显示也比较占位置,有些小伙伴想要删除它,针对这个情况,今日的win10教程就为大伙带来具体的删除方法,有需要的用户可以来本站查看完整的操作步骤吧。win10删除右键图形属性方法1、首先,我们需要通过快捷键【Win+R】来打开电脑的运行功能,此外你可以直接通过,电脑左下角的菜单栏,在搜索框中输入运行,点击出现的结果,也能对于运行功能进行使用。2、打开电脑的运行窗口之后,直接在搜索栏中输入
- 29分钟前 win10 0
-
 正版软件
正版软件
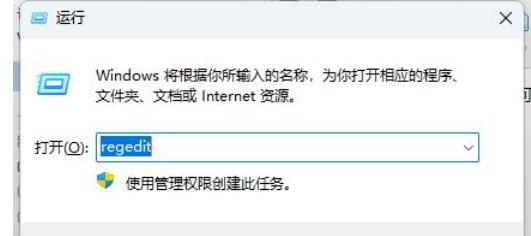
- win11电脑热键怎么重新设置?win11电脑热键设置更改方法
- 我们在使用win11系统的时候会选择设置一些热键来帮助用户们快速的进行设置,但是也有不少的用户们表示自己的热键发生了一些变化,那么win11电脑热键怎么重新设置?用户们可以直接的点击开始菜单下的设置选项来进行操作就可以了。下面就让本站来为用户们来仔细的介绍一下win11电脑热键设置更改方法吧。win11电脑热键设置更改方法1、Win11系统快捷键设置在哪里?首先我们点击【开始菜单】后就可以看到【设置】选项。2、也可以在上方的搜索框输入设置,然后可以固定到任务栏或开始菜单界面。3、当然我们使用鼠标右键点击【
- 44分钟前 win11 0
-
 正版软件
正版软件
- win11打开文件一直转圈怎么办?win11文件夹转圈加载不出解决方法
- 现在越来越多的人都在使用win11系统,而近期有些小伙伴反映说,自己的电脑在打开文件夹的时候,会一直转圈圈,需要等待更多的时间才能够打开查看内容,面对这个问题,多数人都不清楚该如何解决,那么今日的win11教程就来为广大用户们进行解答,接下来让我们一起来看看详细的操作步骤吧。解决方法如下:1、“win+R”快捷键开启运行,输入“regedit”,回车进入。2、进入到注册表编辑器界面后,将“计算机HKEY_LOCAL_MACHINE\SOFTWAR
- 54分钟前 win11 0
-
 正版软件
正版软件
- win11检测工具无法安装怎么办?win11检测工具无法安装问题解析
- 不少的用户们想将自己的电脑安装到win11,但是也有不少的用户们在安装的过程中出现了错误报错的情况,那么win11检测工具无法安装怎么办?用户们可以先下载一个检测软件来看看,下面就让本站来为用户们来为用户们来仔细的介绍一下win11检测工具无法安装问题解析吧。win11检测工具无法安装问题解析1、我们可以先下载一个win11检测软件,看一看我们是哪一个部分不满足win11升级要求。2、点击上方的链接下载这款工具,下载安装后将它打开,然后点击“立即检查”就可以检查了。3、如果我们检查
- 1小时前 02:14 win11 0
最新发布
-
 1
1
- KeyShot支持的文件格式一览
- 1799天前
-
 2
2
- 优动漫PAINT试用版和完整版区别介绍
- 1839天前
-
 3
3
- CDR高版本转换为低版本
- 1984天前
-
 4
4
- 优动漫导入ps图层的方法教程
- 1839天前
-
 5
5
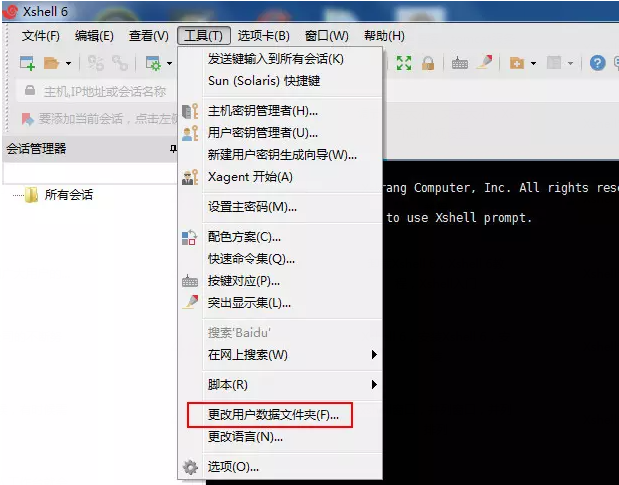
- 修改Xshell默认存储路径的方法教程
- 1851天前
-
 6
6
- ZBrush雕刻衣服以及调整方法教程
- 1835天前
-
 7
7
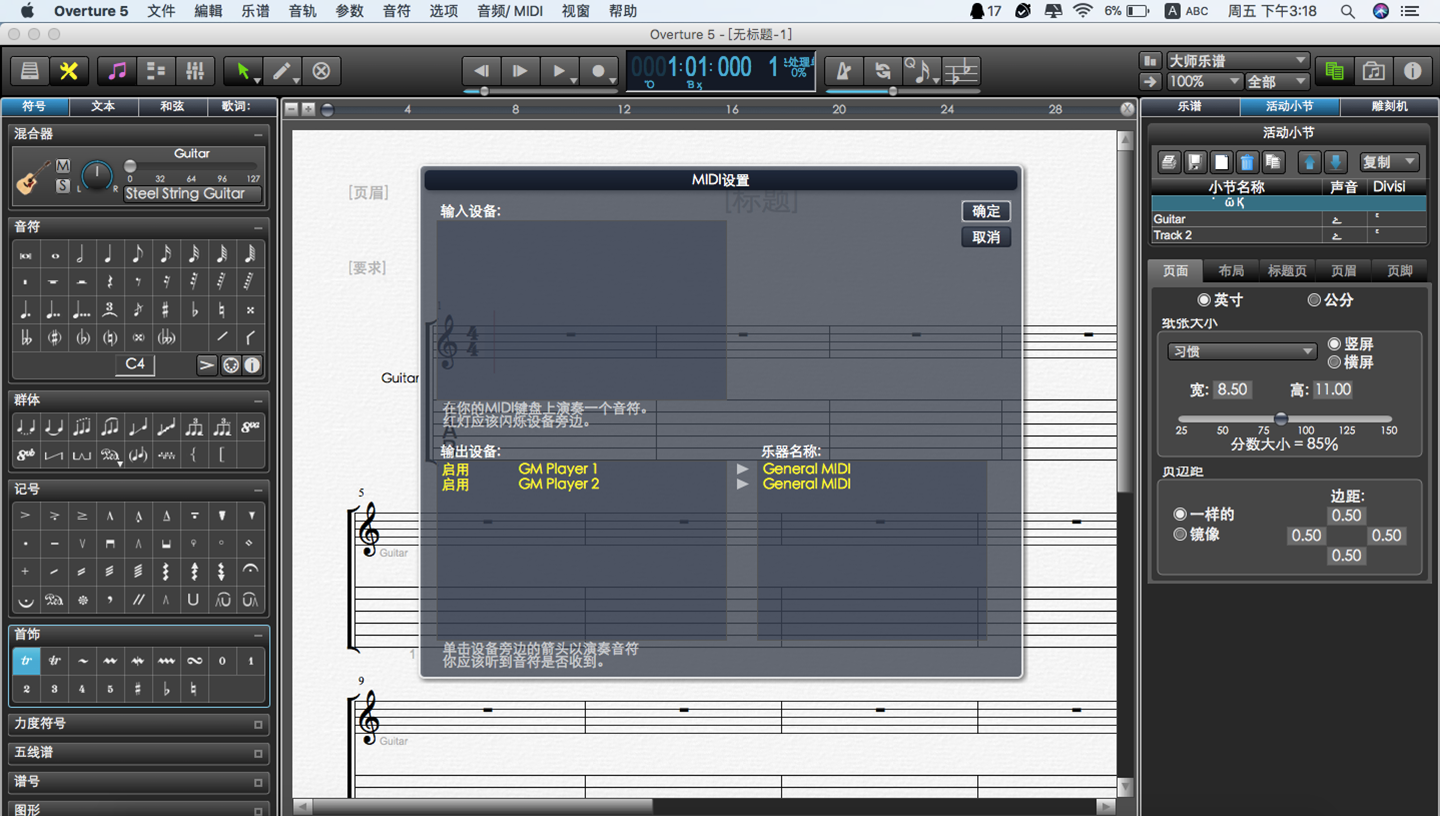
- Overture设置一个音轨两个声部的操作教程
- 1829天前
-
 8
8
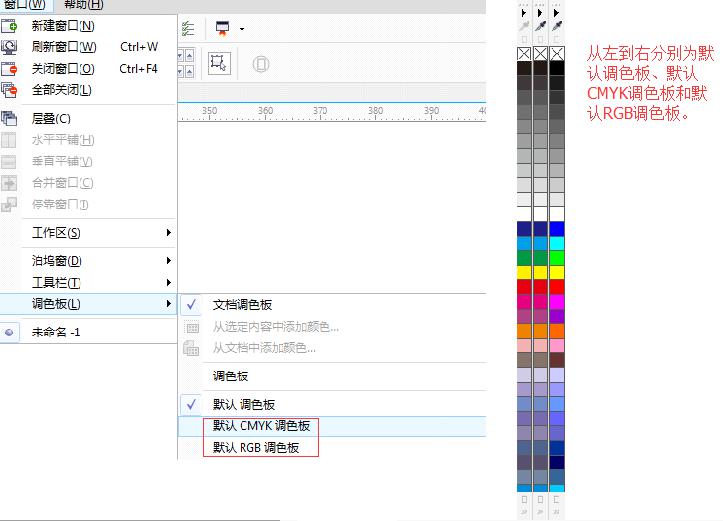
- CorelDRAW添加移动和关闭调色板操作方法
- 1877天前
-
 9
9
- PhotoZoom Pro功能和系统要求简介
- 2005天前
相关推荐
热门关注
-

- Xshell 6 简体中文
- ¥899.00-¥1149.00
-

- DaVinci Resolve Studio 16 简体中文
- ¥2550.00-¥2550.00
-

- Camtasia 2019 简体中文
- ¥689.00-¥689.00
-

- Luminar 3 简体中文
- ¥288.00-¥288.00
-

- Apowersoft 录屏王 简体中文
- ¥129.00-¥339.00